15 July 2019
The Bank of England has announced its selection of Alan Turing as the character to feature on the reverse side of the new £50 banknote, which will come into circulation in 2021.

Alan Mathison Turing OBE FRS (1912–1954) was a mathematician, computer scientist, logician, cryptanalyst, philosopher and theoretical biologist who was instrumental in formalising the concepts of algorithm and computation. Turing worked as a code-breaker during the second world war and is widely accredited with having helped bring an earlier end to the war. The story of his life has had wide implications for changes in political, legal and social attitudes towards human diversity and homosexuality.
In his article ‘On computable numbers, with an application to the Entscheidungsproblem’ (submitted 28 May 1936, published in Proceedings of the London Mathematical Society (2) 42 (1937) 230–265), Turing presented a first model for a general-purpose computer, later to become known as a ‘Turing machine’.
The London Mathematical Society welcomes this great exposure and boost to the public appreciation of mathematics, and is delighted to have contributed to the design of the banknote by giving approval and permission for two mathematical excerpts from this Turing article1 to be included on the new banknote.
The first excerpt is a table from page 240 which provides a schema for succinctly representing Turing machines. The table gives a complete description of how to specify such machines and therefore can be thought of as one of the first examples of a programming language.

The second excerpt, from page 241, is a sequence of Turing machine transitions that helps explain how to encode a Turing machine as a number. The more modern analogue of what Turing describes is how to take an abstract representation of a computer program and convert it into a binary sequence of 0s and 1s so that it can be stored on a disc or in the memory of a computer. The idea that a program can be stored as a number, and used as data (by an operating system) in order to execute the program, is hugely important.
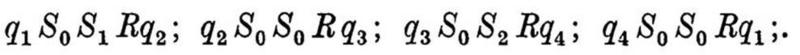
Turing went on further in his article to describe large classes of real numbers whose binary expansions are computable by his machines; to describe a ‘universal machine’ that could serve the purpose of an operating system; and to describe the theoretical limits of his machines. Ultimately, Turing showed that there can be no algorithmic method for determining whether or not a given mathematical statement can be proved in a certain axiomatic system. This proved that David Hilbert's famous Entscheidungsproblem has no solution (which was also proved independently by Alonzo Church).
Alan Turing is the second mathematician to appear on a Bank of England banknote. A £1 banknote in circulation between 1978 and 1988 depicted Sir Isaac Newton. Famous Britons have featured on the reverse of Bank of England banknotes since 1970.
The London Mathematical Society thanks Dr Paul Shafer of the University of Leeds for advice leading to the approval of the mathematical excerpts selected to appear on the banknote, and for providing the above explanations of their relevance in the context of Alan Turing’s article.
1 The Turing article is © London Mathematical Society. All rights reserved. The London Mathematical Society is a not-for-profit Charity registered with the UK Charity Commission. All surplus income from its publishing programme is used to support the mathematics community in the form of research grants, conference grants, prizes, initiatives for early career researchers and the promotion of mathematics.
A collection of Turing's articles in the Proceedings is now available on Wiley Online Library.
